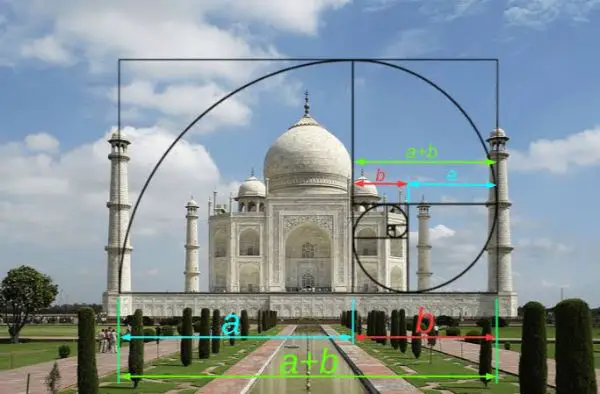
What is all the fuss about the famous golden ratio? Why is it that whenever you lookup for Golden Ratio, all you find is an image that looks like one above. Why are structures or patterns in golden ratio perceived to be aesthetically pleasing? Is there something more to golden ratio than we know of? If you also share this intrigue, let us break it down and try to understand what golden ratio is and why should it be of an importance to us as designers?ood design has been up for debate for as long as we’ve been creating. There are endless forums, social media threads, and in-person conversations about what makes for great design, with everyone contributing their own point of view.
That’s the beauty of design, right? Everyone can interpret it differently. While there will never be a one-size-fits-all approach for design, there is a concrete, mathematical approach that can help us get one step closer to creating amazing design experiences every time: the Golden Ratio. The Golden Ratio is a mathematical ratio you can find almost anywhere, like nature, architecture, painting, and music. When specifically applied to design specifically, it creates an organic, balanced, and aesthetically pleasing composition.
Golden ratio, also known as the golden section, golden mean, or divine proportion, in mathematics, the irrational number (1 + Square root of√5)/2, often denoted by the Greek letter ϕ or τ, which is approximately equal to 1.618. It is the ratio of a line segment cut into two pieces of different lengths such that the ratio of the whole segment to that of the longer segment is equal to the ratio of the longer segment to the shorter segment. The origin of this number can be traced back to Euclid, who mentions it as the “extreme and mean ratio” in the Elements. In terms of present day algebra, letting the length of the shorter segment be one unit and the length of the longer segment be x units gives rise to the equation (x + 1)/x = x/1; this may be rearranged to form the quadratic equation x2 – x – 1 = 0, for which the positive solution is x = (1 + Square root of√5)/2, the golden ratio.
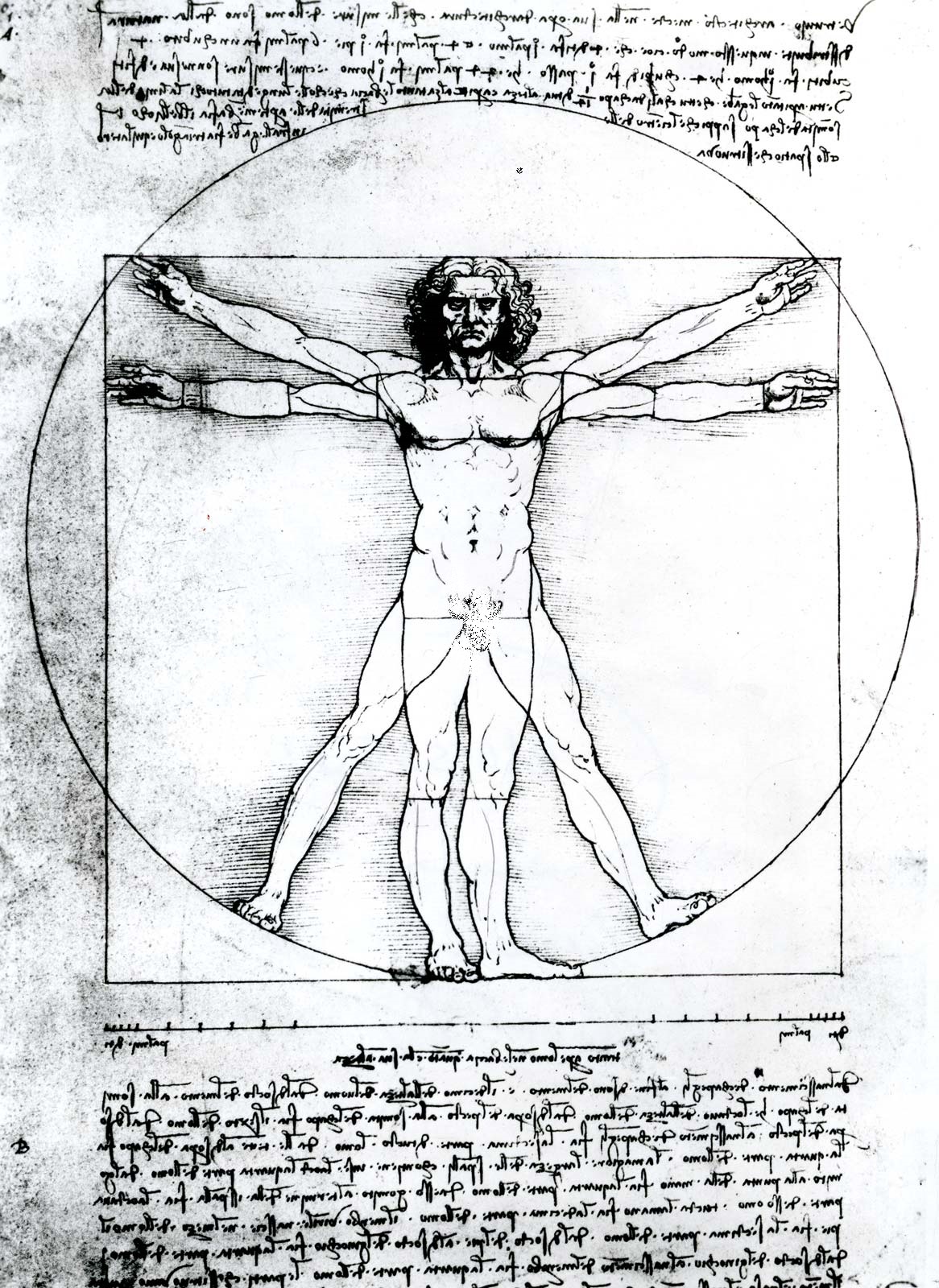
Vitruvian man, a figure study by Leonardo da Vinci (c. 1509) illustrating the proportional canon laid down by the Classical Roman architect Vitruvius; in the Academy of Fine Arts, Venice.
Foto Marburg/Art Resource, New York
The golden ratio occurs in many mathematical contexts. It is geometrically constructible by straightedge and compass, and it occurs in the investigation of the Archimedean and Platonic solids. It is the limit of the ratios of consecutive terms of the Fibonacci number sequence 1, 1, 2, 3, 5, 8, 13,…, in which each term beyond the second is the sum of the previous two, and it is also the value of the most basic of continued fractions, namely 1 + 1/(1 + 1/(1 + 1/(1 +⋯. In modern mathematics, the golden ratio occurs in the description of fractals, figures that exhibit self-similarity and play an important role in the study of chaos and dynamical systems.
Emergence theory predicts a fundamental, natural phenomenon that is so strange yet so prevalent that, with no physics theory having ever explained it, has been largely ignored by the scientific establishment and often seen as the stuff of amateur scientists and hobbyists. This phenomenon is the ubiquity of the golden ratio in nature from the micro (including the Planck scale) to the macro scale. Upon learning of a golden ratio related fact, most scientists will often treat it as a coincidence. However, the statistical probability of the golden ratio’s unrelenting prevalence to such high accuracy is practically zero.
Many of the ways the golden ratio (as well as its rational form, the Fibonacci sequence) appears in nature are well-known – a quick list of examples includes flower petals, seed heads, pine cones, shells, spiral galaxies, hurricanes, faces, DNA molecules and many more. None of this is new. It would be news to many people, however, that the golden ratio makes many precise (100% accuracy) and near-precise (accuracy of and near 99.99…%) appearances in values related to astronomical bodies that are often surprising and interesting. For example it appears, notably, in black hole physics: the golden ratio is precisely the point where a black hole’s modified heat changes from positive to negative, and it is part of the equation for the lower bound on black hole entropy. The golden ratio even relates to the loop quantum gravity parameter to black hole entropy. The three formulas respectively can be seen in this graphic:
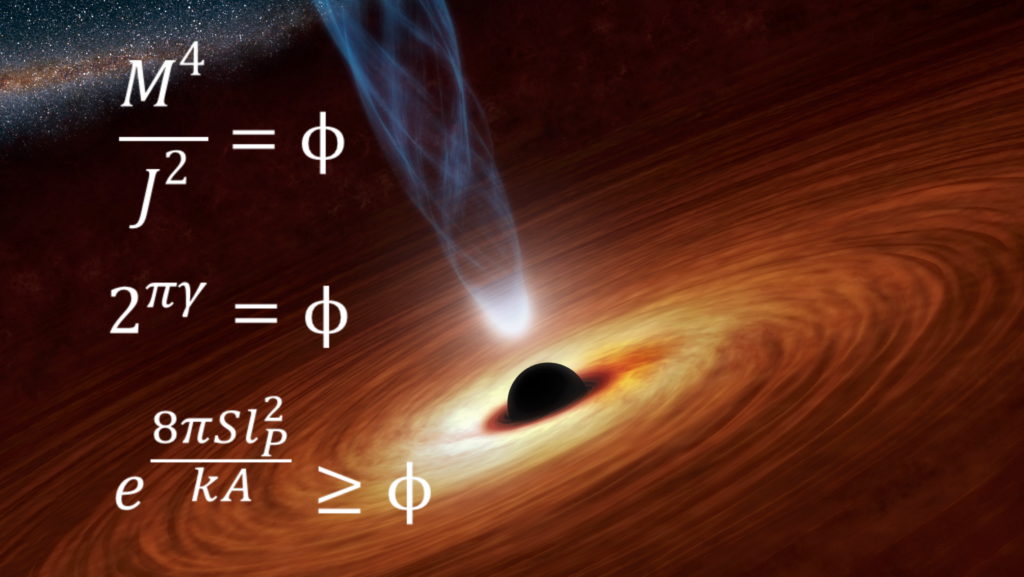
Therefore, the golden ratio may be the fundamental constant of nature.
Black holes are where general relativity and quantum mechanics converge at their limits. Any unification model (“theory of everything”) must include these two theories. In binary matrices, which were used by Heisenberg to describe quantum mechanics, the highest probability non-trivial eigenvalues are the golden ratio, and negative one over the golden ratio. The golden ratio appears fundamentally in quantum mechanics and in black holes. The golden ratio appears in atoms as well. The atomic radius of hydrogen in methane is the Bohr radius over the golden ratio. In 1993 Lucien Hardy of the Perimeter Institute discovered that the probability of entanglement for two particles projected in tandem is the golden ratio over negative 5.
Quasicrystals are golden ratio based geometric languages. They are codes made of geometric symbols. Since reality is three dimensional, we suggest to look first to see if reality might be written in the code 3D quasicrystals. Time and motion could simply be ordered sequences of different 3D quasicrystal configurations, “played” rapidly like a 3D strip of film frames. Ideas like the invariance of the speed of light could be explained using new ideas like an update of the de Broglie electron clock model.
Quasicrystals - Micro/NanoElectronics
Any 3D quasicrystal is really just an interactive network of 1D quasicrystals. The most foundational and simplest 1D quasicrystal, the Fibonacci chain, has two geometric “letters” in its language. (Yes, quasicrystals are languages or codes because they fully meet the definition by having (1) a finite set of two or more symbols, (2) symbol matching rules and (3) syntactical degrees of freedom.) The two geometric letters in a Fibonacci chain quasicrystal are lengths with a ratio of one to the other that is the golden ratio, where the long length has a ratio to the short length that is the same ratio as the long length to the sum of the long + short length. It’s the only ratio in math that switch hits like this.
Languages that have a lot of letters are costly. Imagine if the English language had 23 million letters! Working with it would be mentally difficult and would certainly not conserve choices. Let’s clarify: all choices are not equally resource intensive. Does it require more mental energy to choose between vanilla and chocolate or to choose from 100 delicious flavors of ice cream? Similarly, languages with fewer letters require less resources for each choice of letter. This is one reason why this text you’re reading is expressed as binary code under the secondary level of English words. In a geometric code, like the quasicrystal code nature might be using, a two letter code might be powerful as well. And the only way to get networks of 1D codes to act as an interactive 3D network of 1D codes is to use the golden ratio. Explaining that might take a bit more time and a little math. But suffice it to say that the golden ratio is a powerful tool for building physics.
There have been studies which suggest designs set out using the golden ratio are aethetically pleasing. We can use the golden ratio to help design our paintings and position our subjects.
Who would have thought art and maths could have such a close connection? Luca Pacioli (a contemporary of Leonardo da Vinci) went as far as saying:
“Without mathematics there is no art.”
Georges Seurat, Bathers at Asnières, 1884
In this painting by Georges Seurat, the golden ratio appears to have been used throughout the painting - to define the horizon, to place points of interest and to create balance in what would appear to be a very active scene.
Georges Seurat also seems to have used the golden ratio in this painting. Notice the positioning of the jetty, the sail mast and the horizon.
Curiously enough, we even find golden ratio relationships in the solar system and universe. The diameters of the Earth and Moon form a triangle whose dimensions are based on the mathematical characteristics of phi. The distances of the planets from the sun correlate surprisingly closely to exponential powers of Phi. The beautiful rings of Saturn are very close in dimension to the golden ratio of the planet’s diameter. NASA released findings in 2003 that the shape of the Universe is a dodecahedron based on Phi.
Appearances of Phi, the Golden Ratio, in the Solar System
The Golden Ratio continues to open new doors in our understanding of life and the universe. It appeared in Roger Penrose’s discovery in the 1970’s of “Penrose Tiles,” which allowed surfaces to be tiled in five-fold symmetry, a task previously thought impossible. It appeared again in the 1980’s in the three-dimensional molecular arrangement of quasi-crystals, a newly discovered form of matter. As we enter the 21st century, Phi seems to be having a rebirth in integrating knowledge across a wide variety of fields of study, including time and quantum physics.
The description of this golden proportion as the Divine proportion is perhaps fitting because it is seen by many as a door to a deeper understanding of beauty and spirituality in life, unveiling a hidden harmony or connectedness in so much of what we see. That’s an incredible role for a single number to play, but then again this one number has played an incredible role in human history and in the foundations of life itself. The line between its mathematical and mystical aspects is thus not easily drawn.
Golden ratio in Meditation
Phi does not appear explicitly in the Bible or other ancient scriptures, yet we find that the dimensions given by God to Noah for the Ark and to Moses for the Ark of the Covenant both reflect a 5 to 3 proportion, Fibonacci numbers with a ratio of 1.666, and a reasonably close approximation to Phi. The Kaaba, the most sacred site of Islam in Mecca, is located very close to the golden ratio of the distance between the Earth’s north and south poles. Curiously enough, even the symbol for Phi, a circle with a line drawn through it, can be thought to represent a zero, or void, divided by one, or Unity, to create beauty, analogous to God creating the universe from nothing.
The term "golden section" (in German, goldener Schnitt or der goldene Schnitt) seems to first have been used by Martin Ohm in the 1835 2nd edition of his textbook Die Reine Elementar-Mathematik (Livio 2002, p. 6). The first known use of this term in English is in James Sulley's 1875 article on aesthetics in the 9th edition of the Encyclopedia Britannica. The symbol phi ("phi") was apparently first used by Mark Barr at the beginning of the 20th century in commemoration of the Greek sculptor Phidias (ca. 490-430 BC), who a number of art historians claim made extensive use of the golden ratio in his works (Livio 2002, pp. 5-6). Similarly, the alternate notation tau is an abbreviation of the Greek tome, meaning "to cut."
In the Season 1 episode "Sabotage" (2005) of the television crime drama NUMB3RS, math genius Charlie Eppes mentions that the golden ratio is found in the pyramids of Giza and the Parthenon at Athens. Similarly, the character Robert Langdon in the novel The Da Vinci Code makes similar such statements (Brown 2003, pp. 93-95). However, claims of the significance of the golden ratio appearing prominently in art, architecture, sculpture, anatomy, etc., tend to be greatly exaggerated.
phi has surprising connections with continued fractions and the Euclidean algorithm for computing the greatest common divisor of two integers.
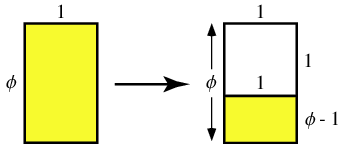
Given a rectangle having sides in the ratio 1:x, phi is defined as the unique number x such that partitioning the original rectangle into a square and new rectangle as illustrated above results in a new rectangle which also has sides in the ratio 1:x (i.e., such that the yellow rectangles shown above are similar). Such a rectangle is called a golden rectangle, and successive points dividing a golden rectangle into squares lie on a logarithmic spiral, giving a figure known as a whirling square.
Based on the above definition, it can immediately be seen that
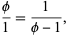
giving
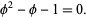
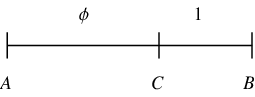
Euclid ca. 300 BC gave an equivalent definition of phi by defining it in terms of the so-called "extreme and mean ratios" on a line segment, i.e., such that
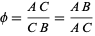
for the line segment AB illustrated above (Livio 2002, pp. 3-4). Plugging in,
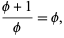
and clearing denominators gives
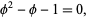
which is exactly the same formula obtained above (and incidentally means that phi is an algebraic number of degree 2.) Using the quadratic equation and taking the positive sign (since the figure is defined so that phi>1) gives the exact value of phi, namely
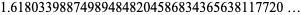
(OEIS A001622). Prime numbers appearing in consecutive digits of the decimal expansion (starting with the first) are known as phi-primes.
In an apparent blatant misunderstanding of the difference between an exact quantity and an approximation, the character Robert Langdon in the novel The Da Vinci Code incorrectly defines the golden ratio to be exactly 1.618 (Brown 2003, pp. 93-95).
The legs of a golden triangle (an isosceles triangle with a vertex angle of 36 degrees) are in a golden ratio to its base and, in fact, this was the method used by Pythagoras to construct phi. The ratio of the circumradius to the length of the side of a decagon is also phi,
Bisecting a (schematic) Gaullist cross also gives a golden ratio (Gardner 1961, p. 102).
Exact trigonometric formulas for phi include
The golden ratio is given by the series
(B. Roselle). Another fascinating connection with the Fibonacci numbers is given by the series
A representation in terms of a nested radical is
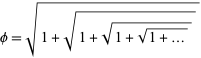
(Livio 2002, p. 83). This is equivalent to the recurrence equation
with a_1=1, giving lim_(n->infty)a_n=phi.
is the "worst" real number for rational approximation because its continued fraction representation
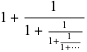
(OEIS A000012; Williams 1979, p. 52; Steinhaus 1999, p. 45; Livio 2002, p. 84) has the smallest possible term (1) in each of its infinitely many denominators, thus giving convergents that converge more slowly than any other continued fraction. In particular, the convergents x_n=p_n/q_n are given by the quadratic recurrence equation
with 
, which has solution
where F_n is the nth Fibonacci number. This gives the first few convergents as 1, 2, 3/2, 5/3, 8/5, 13/8, 21/13, 34/21, ... (OEIS A000045 and A000045), which are good to 0, 0, 0, 1, 1, 2, 2, 2, 3, 3, 4, 4, 5, 5, 5, ... (OEIS A114540) decimal digits, respectively.
As a result,
as first proved by Scottish mathematician Robert Simson in 1753 (Wells 1986, p. 62; Livio 2002, p. 101).
The golden ratio also satisfies the recurrence relation
Taking n=1 gives the special case
Treating above as a linear recurrence equation
in , setting 
and 
, and solving gives
as expected. The powers of the golden ratio also satisfy
where 
is a Fibonacci number (Wells 1986, p. 39).
The sine of certain complex numbers involving phi gives particularly simple answers, for example
(D. Hoey, pers. comm.).
In the figure above, three triangles can be inscribed in the rectangle ABCD of arbitrary aspect ratio 1:r such that the three right triangles have equal areas by dividing AB and BC in the golden ratio. Then
which are all equal. The converse is also true, namely if the adjacent sides of a rectangle are divided in any ratio and connected in the same way, then if the areas of the three outer triangles are all equal, both divided sides are in the golden ratio (D. J. Lewis, pers. comm., Jun. 11, 2009).
The substitution system
gives
giving rise to the sequence
(OEIS A003849). Here, the zeros occur at positions 1, 3, 4, 6, 8, 9, 11, 12, ... (OEIS A000201), and the ones occur at positions 2, 5, 7, 10, 13, 15, 18, ... (OEIS A001950). These are complementary Beatty sequences generated by |_nphi_| and |_nphi^2_|. This sequence also has many connections with the Fibonacci numbers. It is plotted above (mod 2) as a recurrence plot.
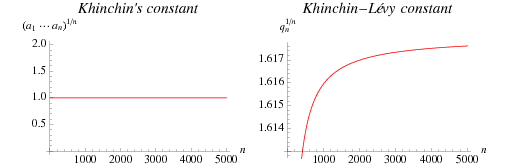
Let the continued fraction of phi be denoted [a_0;a_1,a_2,...] and let the denominators of the convergents be denoted q_1, q_2, ..., q_n. As can be seen from the plots above, the regularity in the continued fraction of phi means that phi is one of a set of numbers of measure 0 whose continued fraction sequences do not converge to Khinchin's constant or the Lévy constant.
The golden ratio has Engel expansion 1, 2, 5, 6, 13, 16, 16, 38, 48, 58, 104, ... (OEIS A028259).
Steinhaus (1999, pp. 48-49) considers the distribution of the fractional parts of 
in the intervals bounded by 0, 1/n, 2/n, ..., (n-1)/n, 1, and notes that they are much more uniformly distributed than would be expected due to chance (i.e., 
is close to an equidistributed sequence). In particular, the number of empty intervals for n=1, 2, ..., are a mere 0, 0, 0, 0, 0, 0, 1, 0, 2, 0, 1, 1, 0, 2, 2, ... (OEIS A036414). The values of n for which no bins are left blank are then given by 1, 2, 3, 4, 5, 6, 8, 10, 13, 16, 21, 34, 55, 89, 144, ... (OEIS A036415). Steinhaus (1983) remarks that the highly uniform distribution has its roots in the continued fraction for 
.
The sequence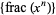 
, of power fractional parts, where 
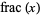is the fractional part, is equidistributed for almost all real numbers 
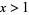, with the golden ratio being one exception.
Salem showed that the set of Pisot numbers is closed, with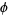 
the smallest accumulation point of the set (Le Lionnais 1983).